Robustnost analytické metody a Hodnocení linearity
HPLC.cz: Robustnost analytické metody a Hodnocení linearity
Definice
Anglický ekvivalent pro robustnost je Ruggedness nebo Robustness. První zmínka o robustnosti – Youden (1961): "… analytical process need to be „rugged“…
Robustnost analytického postupu je mírou jeho kapacity zůstat netečný vůči malým, ale záměrným změnám parametrů metody a poskytuje informaci o jeho spolehlivosti během běžného používání.
Robustnost je tudíž schopnost metody být „netečná k mírným (a nevyhnutelným) odchylkám od některé obvyklé rutinní činnosti“ (W.J. Youden, Statistical techniques for collaborative tests. Statistical manual of the AOAC, Washington DC.
Dále může být robustnost definována jako míra vlivu mírného kolísání úrovně jednotlivých parametrů na výsledek analytického stanovení. Definice robustnosti je v každém protokolu jiná (ICH, FDA, PhEur, JP, USP).
Srozumitelná definice je následující: Robustnost metody je definována jako míra kapacity metody při jejím reprodukování za nepatrně změněných podmínek. Změna podmínek může nastat pro případ mezilaboratorních zkoušek (jiná laboratoř, analytik, instrument = RUGGEDNESS) nebo změnou podmínek v jedné laboratoři (teplota, koncentrace, doba extrakce = ROBUSTNESS).
Zde si dovolím nadefinovat svou vlastní verzi
Robustnost metody je taková vlastnost metody, kdy malou změnou jejich parametrů, poskytuje metoda pořád správné a přesné výsledky.
Největší problém při ověřování robustnosti podle výše uvedených definic je definování míry (velikosti) odchylky (parametru) resp. mírného kolísání úrovně. Nebyla stanovena žádná kriteria (velikost odchylky), ale obecně by se mělo vycházet z nejistoty měření nebo předpisů (PhEur, JP, USP).
Co je cílem resp. výsledkem ověření robustnosti metody?
Výsledkem není závěr, že metoda je robustní nebo nerobustní, ale výsledkem robustnosti je informace, jaké parametry metody jsou kritické vyžadující pečlivou kontrolu. Výsledkem robustnosti může být také interval kritických parametrů metody, ve kterém metoda poskytuje nejmenší chyby měření.
Experimental design
Při ověřování robustnosti existují dva zásadní přístupy k tomuto problému: univariační (jednorozměrná) analýza dat nebo tzv. multivariační (vícerozměrná) analýza dat.
Univariační (jednorozměrná) analýza dat
Postup: Mění se jeden parametr (faktor) v čase a ostatní parametry (faktory) zůstávají fixní a sleduje se jak ovlivní výsledek. Poté se experiment zopakuje s dalším parametrem – tzv. přístup OFAT (One Factor At Time).
Příklad: Nechť máme 3 parametry (A,B,C) a sledujeme pouze dva extrémy každého parametru: (-) a (+) a ostatní zůstávají neměnné (0) atd …, pak metodou OFAT dostaneme následující kombinace:
_l.webp) HPLC.cz: Přístup OFAT (One Factor At Time)
HPLC.cz: Přístup OFAT (One Factor At Time)
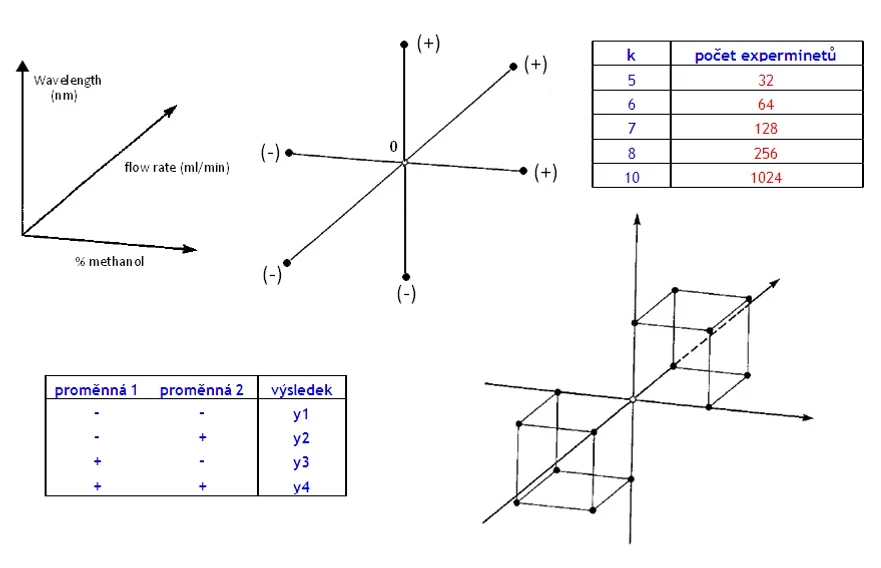
Pro počet experimentů obecně platí: 2*k+1. Mluvíme o tzv. hvězdicovém schématu („
 HPLC.cz: Hvězdicové schéma
HPLC.cz: Hvězdicové schéma
Další z používaných algoritmů je tzv. zrcadlové faktorové schéma („
 HPLC.cz: Zrcadlové faktorové schéma
HPLC.cz: Zrcadlové faktorové schéma
Pro počet experimentů obecně platí: 2(2k+1)* a dostáváme následující kombinace:
-2_l.webp) HPLC.cz: Přístup OFAT (One Factor At Time)
HPLC.cz: Přístup OFAT (One Factor At Time)
Multivariační (vícerozměrná) analýza dat
Robustnost metody vůči malým změnám se testuje na základě plánovaných pokusů (úplných nebo zkrácených).
Příklad: Pro jednoduchost = výsledek ovlivní pouze dvě proměnné veličiny (např. teplota a čas; veličiny mohou být plynule měnitelné nebo i binární). Při experimentu převádíme všechny proměnné na binární: + a – (u plynule proměnných tedy volíme dva stavy: nominální a extrémní a počet úrovní proměnné veličiny je tedy 2). Plán pak lze popsat takto:
 HPLC.cz: Plán testování
HPLC.cz: Plán testování
Velice časově náročné, v případě že chceme sledovat vliv 4 proměnných pak dostaneme 2⁴ = 16 experimentů, které je nutné udělat. Obecně platí: 2ᵏ. Nárůst poštu experimentů je patrný z tabulky:
 HPLC.cz: Nárůst poštu experimentů
HPLC.cz: Nárůst poštu experimentů
Při optimalizaci postupu pro silanizaci silikagelu pro HPLC museli autoři posoudit 23 proměnných. V případě, že by jeden experiment trval 10 minut, pak k provedení úplného plánu bylo zapotřebí 160 let nepřetržité práce.
Z důvodu takto velkých počtů experimentů se zanedbává možnost ovlivňování jednotlivých proměnných => tzv. neúplné faktorové plány (fiktivní proměnné) s různými algoritmy. Postup pro testování pomocí Plackett-Burmanova plánu je popsán zde.
Existuje ještě řada dalších postupů a algoritmů hodnocení, pro úplnost uvádím Dongův, Vander Heydenův, Youdenův algoritmus.
Hodnocení linearity
Linearita je chápána jako přímková závislost mezi dvěma náhodnými proměnnými, tj. odezvou instrumentace (analytickým signálem) a koncentrací analytu. V současné době se k hodnocení linearity používá téměř výhradně korelační koeficient. Korelační koeficient R měří stupeň korelace a ne linearitu. Závisí na rozložení bodů na přímce! Proto se mohou používat další testy, které daleko více vypovídají o linearitě:
QC koeficient
Pro QC koeficient platí:
 HPLC.cz: QC koeficient
HPLC.cz: QC koeficient
kde ȳ jsou predikované (odhadnuté, vyrovnané) hodnoty yᵢ, tj. hodnoty vypočtené z regresní rovnice.
QC koeficient se používá v kombinaci s korelačním koeficientem a linearita se obecně považuje za prokázanou, když R > 0.99 a QC < 5%. (14)
Analýza rozptylu (ANOVA) na těsnost proložení
Používá se tam, kde je k dispozici řada minimálně 6 standardů se 2-3 opakovanými měřeními pro každou koncentrační úroveň. Pro F platí:
-na-tesnost-prolozeni_l.webp) HPLC.cz: Analýza rozptylu (ANOVA) na těsnost proložení
HPLC.cz: Analýza rozptylu (ANOVA) na těsnost proložení
kde k je počet koncentračních úrovní a n je celkový počet měření, SSPE je suma čtverců reziduí zapříčiněná nepřesným měřením a SSLOF je suma čtverců reziduí zapříčiněná nedostatečným proložením dat. Linearita se obecně považuje za prokázanou, když F < Ft(P=0,95; f=k-2; n-k).
T-test na významnost kvadratického členu
U modelu regresní přímky lze ověřit předpoklad linearity testováním významnosti kvadratického členu pro rovnici y = a + bx+c²x. Testovací kritérium má tvar:
 HPLC.cz: T-test na významnost kvadratického členu
HPLC.cz: T-test na významnost kvadratického členu
kde RSCk jako reziduální součet čtverců pro kvadratický model a RSCL jako reziduální součet čtverců pro lineární model. Linearita se obecně považuje za prokázanou, když FL < Ft(P=0,95; f=1; n-3).
Přehled metodiky pro transfer analytických metod publikoval P. Araujo. (15)
Literatura
- Jones K., J. Chromatogr. 392 (1987) 1.
- Plackett R.L., Burmann J.P., Biometrika 33 (1946) 305.
- M. Mulholland, TRAC, 7 (1988) 383.
- Y. Vander Heyden, F. Questier and D.L. Massart, J. Pharm. Biomed. Anal. 8 (1998) 43.
- van de Vaart F.J. et al., Het Pharmaceutisch Weekblad 127 (1992) 1229.
- M. Mulholland, J. Waterhouse, J. Chromatogr. 395 (1987) 539.
- Y. Vander Heyden, C. Hartmann, D.L. Massart; L. Michel, P. Kiechle, F. Erni, Anal. Chim. Acta 316 (1995) 15.
- Y. Vander Heyden, F. Questier, D.L. Massart, J. Pharm. Biomed. Anal. 17 (1998) 153.
- Y. Vander Heyden, D.L. Massart; Y. Zhu, J. Hoogmartens, J. De Beer; J. Pharm. Biomed. Anal. 14 (1996) 1313.
- Y. Vander Heyden, C. Hartmann, D.L. Massart, P. Nuyten, A.M. Hollands, P. Schoenmakers, J. Chromatogr. A 756 (1996) 89.
- Y. Vander Heyden, M. Jimidar, E. Hund, N. Niemeijer, R. Peeters, J. Smeyers-Verbeke, D.L. Massart, J. Hoogmartens, J. Chromatogr. A, 845 (1999) 145.
- ICH Harmonised Tripartite Guideline prepared within the Third International Conference on Harmonisation of Technical Requirements for the Registration of Pharmaceuticals for Human Use (ICH), Validation of Analytical Procedures : Methodology, 1996, 1-8.
- Youden W.J., Mater. Res. Stand. 1 (1961) 863.
- J. Van Loco, M. Elskens, Ch. Croux, H. Beernaert: Accredit. Qual. Assur. 7 (2002) 281-285.
- P. Araujo: J. Chrom. B. 877, 2224 (2009).




